2.4. Advanced Topics¶
2.4.1. Customized Morphing Operators¶
Let us now get back to the concept of chemical operators and
show an example implementation of a simple new operator, as we promised
while we talked about the basics of molecular morphing
in the very first section of this tutorial.
First, about the operator itself. We will define a new chemical operator that we would like to incorporate into the workflow we developed previously. This operator will give us the ability to take ‘shortcuts’ in chemical space by adding certain fragments rather than just atoms. With a little help from the RDKit library, such operator could be defined as follows:
1from rdkit import Chem
2from molpher.core import MolpherMol, MolpherAtom
3from molpher.core.morphing.operators import MorphingOperator
4from molpher.random import get_random_number
5
6class AddFragment(MorphingOperator):
7
8 def __init__(self, fragment, open_atoms_frag, oper_name):
9 super(AddFragment, self).__init__()
10 self._name = oper_name
11 self._fragment = fragment
12 self._open_atoms_frag = open_atoms_frag
13 self._orig_rdkit = None
14 self._open_atoms = []
15
16 def setOriginal(self, mol):
17 super(AddFragment, self).setOriginal(mol)
18 if self.original:
19 self._orig_rdkit = self.original.asRDMol()
20 self._open_atoms = []
21
22 for atm_rdkit, atm_molpher in zip(self._orig_rdkit.GetAtoms(), self.original.atoms):
23 free_bonds = atm_rdkit.GetImplicitValence()
24 if free_bonds >= 1 and not (MolpherAtom.NO_ADDITION & atm_molpher.locking_mask):
25 self._open_atoms.append(atm_rdkit.GetIdx())
26
27 def morph(self):
28 combo_mol = Chem.EditableMol(Chem.CombineMols(
29 self._orig_rdkit
30 , self._fragment
31 ))
32 atom_orig = self._open_atoms[get_random_number(0, len(self._open_atoms)-1)]
33 atom_frag = len(self.original.atoms) + self._open_atoms_frag[get_random_number(0, len(self._open_atoms_frag)-1)]
34 combo_mol.AddBond(atom_orig, atom_frag, order=Chem.rdchem.BondType.SINGLE)
35 combo_mol = combo_mol.GetMol()
36 Chem.SanitizeMol(combo_mol)
37
38 ret = MolpherMol(other=combo_mol)
39 for atm_ret, atm_orig in zip(ret.atoms, self.original.atoms):
40 atm_ret.locking_mask = atm_orig.locking_mask
41
42 return ret
43
44 def getName(self):
45 return self._name
A new chemical operator must implement the MorphingOperator abstract class
and define three methods:
1.
setOriginal()– used to set the structure that will be modified during morphing. Its purpose is to figure out what atoms in the molecule can be changed and what restrictions apply. In our example, we just find all atoms that have at least one implicit bond to a hydrogen atom. We save the indices of such atoms in the_open_atomsmember of ourAddFragmentclass. Note that we also made sure that no locked atoms were added to the list as well.2.
morph()– This is the method where the original molecule is changed to a new one. In our example, we randomly pick one atom from the original molecule and one from our fragment. Then we connect them. After we are done, we make sure to sanitize the result and also transfer any locks from the original molecule to the new one.3.
getName()– This method is also required to implement and should return a string with the name of the operator. This is then saved to theparent_operatormember of theMolpherMolinstance returned by themorphmethod.
Let’s test if our new operator works as expected:
1captopril = MolpherMol("captopril.sdf")
2frag = Chem.MolFromSmiles('c1ccccc1')
3add_frag = AddFragment(frag, [1], "Add Benzene")
4add_frag.setOriginal(captopril)
5depict(add_frag.morph())
Output:
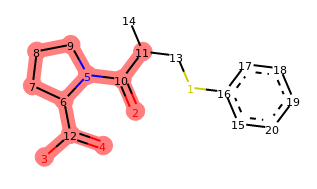
Indeed, our operator seems to be doing what we designed it to do. If you run the last line of this code a few times, you should see different variations of captopril with a benzene ring attached at random positions. The locked positions should always be excluded.
See also
We omit the source of the depict method, which is too long
and not relevant at the moment. It is defined in the example Jupyter Notebook, though (
available for download
or rendered).
The only thing that remains is to use our operator in the context of an exploration
tree. Every tree has the morphing_operators property which stores
the morphing operators currently in use. All we need to do,
is to write a new list of operators and include the one
we just defined:
1from molpher.core import ExplorationTree as ETree
2
3captopril = MolpherMol("captopril.sdf")
4enalapril = MolpherMol("O=C(O)[CH]2N(C(=O)[CH](N[CH](C(=O)OCC)CCc1ccccc1)C)CCC2")
5tree = ETree.create(source=captopril, target=enalapril)
6tree.morphing_operators = tree.morphing_operators + (add_frag,)
Then we can run the exploration as before (Listing 2.8):
1class FindClosest:
2
3 def __init__(self):
4 self.closest_mol = None
5 self.closest_distance = None
6
7 def __call__(self, morph):
8 if not self.closest_mol or self.closest_distance > morph.dist_to_target:
9 self.closest_mol = morph
10 self.closest_distance = morph.dist_to_target
11
12closest_info = FindClosest()
13while not tree.path_found:
14 tree.generateMorphs()
15 tree.sortMorphs()
16 tree.filterMorphs()
17 tree.extend()
18 tree.prune()
19 tree.traverse(closest_info)
20 print('Generation #', tree.generation_count, sep='')
21 print('Molecules in tree:', tree.mol_count)
22 print(
23 'Closest molecule to target: {0} (Tanimoto distance: {1})'.format(
24 closest_info.closest_mol.getSMILES()
25 , closest_info.closest_distance
26 )
27 )
Output (some contents omitted):
Generation #1
Molecules in tree: 21
Closest molecule to target: CC(CSC1=CC=CC=C1)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.484375)
Generation #2
Molecules in tree: 105
Closest molecule to target: CC(CCC1=CC=CC=C1)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.3035714285714286)
Generation #3
Molecules in tree: 205
Closest molecule to target: CC(CCC1=CC=CC=C1)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.3035714285714286)
...
Generation #10
Molecules in tree: 787
Closest molecule to target: C=C(CC)C(CCC1=CC=CC=C1)NC(C)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.21666666666666667)
Generation #11
Molecules in tree: 811
Closest molecule to target: CC(NC(CCC1=CC=CC=C1)C(=O)OCN)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.13793103448275867)
Generation #12
Molecules in tree: 838
Closest molecule to target: CCOC(=O)C(CCC1=CC=CC=C1)NC(C)C(=O)N1CCCC1C(=O)O (Tanimoto distance: 0.0)
There is literally no change to our morphing code. We only added one more operator to the tree prior to running it. We can see that the algorithm only needs 12 iterations to converge this time (the original algorithm above needed 44). Therefore, our shortcut was successful and we managed to spare the algorithm the tedious aromatic ring creation we commented on before.
Let’s take a look at the generated path now:
show_mol_grid(tree.fetchPathTo(tree.params['target']))
Output:
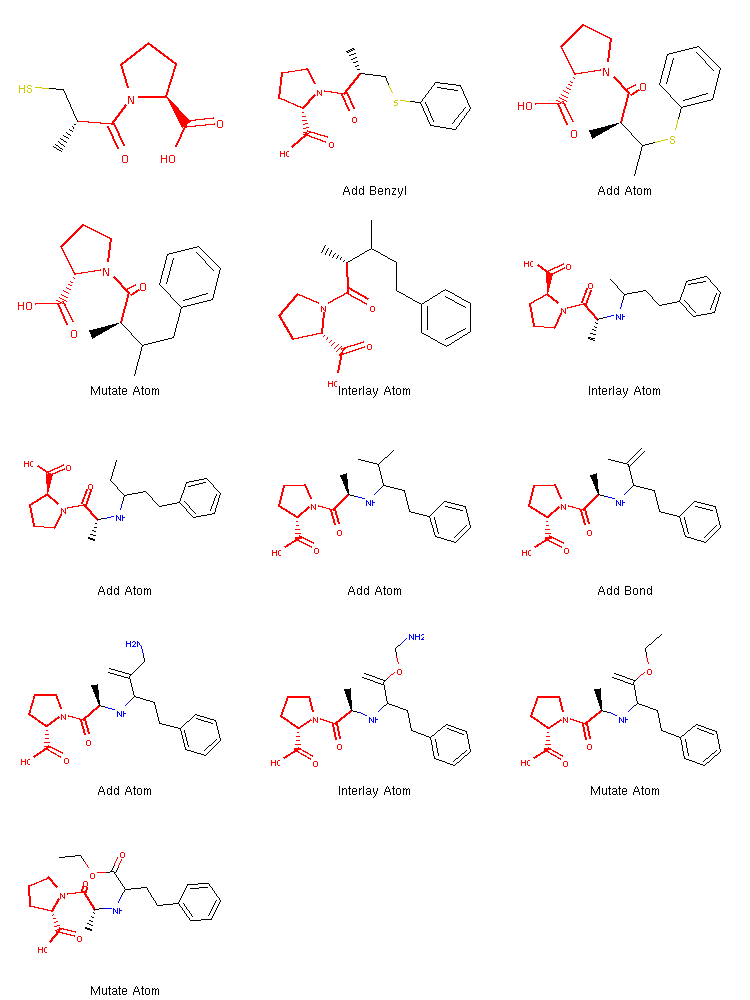
We can see that once the benzene ring is incorporated at the very beginning, the algorithm quickly finds the operations needed to create the target structure.
Since there is some randomization involved in this process, running the algorithm for a second time results in a different path:
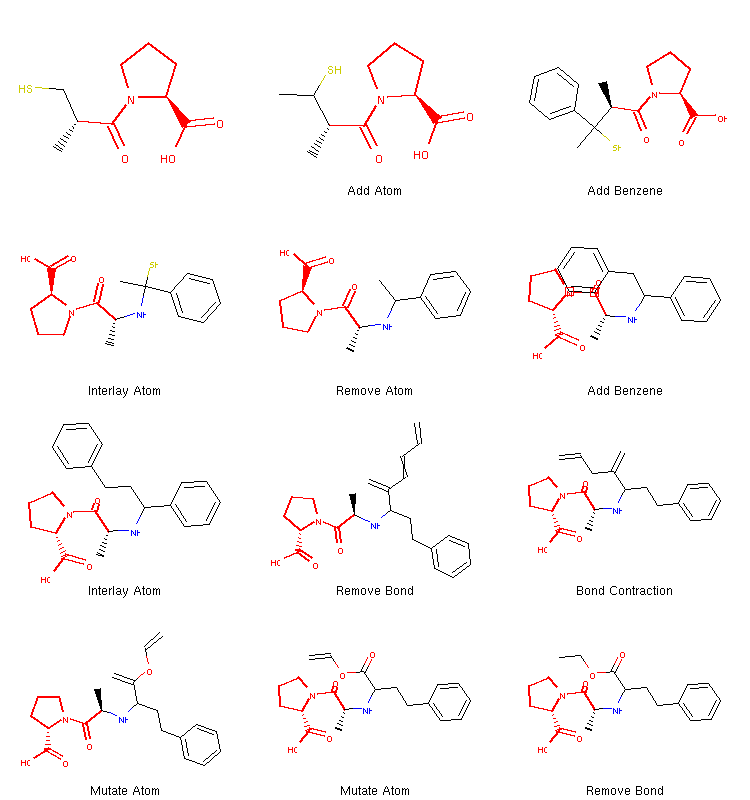
We can see that this time the algorithm decided to take a different route. It added two benzene rings quite early and then proceeded to break one of them down to create the final structure. Therefore, running the same algorithm multiple times can lead to different coverage of chemical space and different structures can be discovered this way.
2.4.2. Tree Operations¶
In the previous section, we used some methods of the ExplorationTree
to generate new morphs and extend it, but also to prune it.
These methods, however, have one thing in common. They work with a single
exploration tree instance and change it somehow. Therefore, their functionality
can be defined with an interface and that is what we will cover in this section,
the tree operation interface and how to use it.
We call every action that is performed on an exploration tree a tree operation.
This concept is represented in the library with the TreeOperation
abstract class and it becomes useful when we need to control
several exploration trees at once or if we just prefer to separate the tree itself from the
logic of our exploration algorithm.
Note
Tree operations were mainly created to house different parts of the exploration algorithm
and to make them more encapsulated and configuration more intuitive. However, this transition is still
far from complete so most of the built-in operations take their parameters from the params property,
which is defined globally for the tree in question. Most of these parameters will eventually be
encapsulated by their respective operations, though.
When we have defined our own operation, we can run it on a tree by supplying it to the
runOperation() method. Here is an example of how to define a customized filtering
procedure (similar to the one used before) and incorporate it
into an exploration algorithm:
1import molpher
2from molpher.core.operations import *
3from molpher.core import MolpherMol, ExplorationTree as ETree
4
5class MyFilterMorphs(TreeOperation):
6 """
7 A custom tree operation that accepts
8 only the first ten morphs after
9 the list of candidates is sorted.
10 """
11
12 def __call__(self):
13 """
14 This method is called automatically by the tree.
15 The tree this operation is being run on is accessible
16 from the 'tree' member of the class.
17 """
18
19 self.tree.candidates_mask = [
20 True if idx < 20 and self.tree.candidates[idx].sascore < 6
21 else False
22 for idx, x in enumerate(self.tree.candidates_mask)
23 ]
24
25cocaine = MolpherMol('CN1[CH]2CC[CH]1[CH](C(OC)=O)[CH](OC(C3=CC=CC=C3)=O)C2')
26procaine = MolpherMol('O=C(OCCN(CC)CC)c1ccc(N)cc1')
27tree = ETree.create(source=cocaine, target=procaine) # create the tree
28
29# list of tree operations, defines one iteration
30iteration = [
31 GenerateMorphsOper()
32 , SortMorphsOper()
33 , MyFilterMorphs() # our custom filtering procedure
34 , ExtendTreeOper()
35 , PruneTreeOper()
36]
37
38# apply the operations in the list one by one
39for oper in iteration:
40 tree.runOperation(oper)
41
42# observe the results
43print(tree.generation_count)
44print(len(tree.leaves))
Output:
1
18
See also
This and other advanced examples are included in a Jupyter Notebook
which can be downloaded from here
or viewed directly.
Except for the source and target molecule, this algorithm is similar to what
we have seen before, but this time we used operations instead of calling
the corresponding methods on the tree. We used a customized operation for the filtering step
by creating a subclass of the TreeOperation
abstract class and we overrode its
__call__() method with the implementation we want.
Each operation can have a tree associated with it, but it is not necessary
(we had no problems initializing the operations without a tree in the previous example).
We can verify if a tree is associated with an operation by calling
its getTree()
method or accessing the TreeOperation.tree attribute of the class.
If there is no tree associated with the instance, they both return None.
We can set the tree to operate on by writing into the TreeOperation.tree
attribute or calling the TreeOperation.setTree method. Then the operation
becomes callable (calling it will result in a RuntimeError).
2.4.2.1. Built-in Operations¶
Warning
This section is not yet complete because
most of these operations will change their interface in the feature.
We only describe the TraverseOper
class, which has more practical use than the others and its
interface will not undergo much change in the future. For the other operations,
we kindly refer the reader to their respective documentation pages.
In this section, we describe the few operations the library inherited from Molpher:
They are all derived from TreeOperation and contain
the full set of operations performed on a tree in
the original Molpher algorithm as published in 1. Therefore, the original algorithm can be
implemented using those operations.
2.4.2.1.1. Traversing the Tree¶
A special place among these operations belongs to the TraverseOper
class. It does not directly implement a part
of a morphing algorithm, but serves as a means of traversing molecules in a tree and reading/modifying them
as needed:
1from molpher.core.operations.callbacks import TraverseCallback
2
3class MyCallback(TraverseCallback):
4 """
5 This callback just prints some information
6 about the molecules in the tree.
7
8 """
9
10 def __call__(self, morph):
11 """
12 Method called on each morph in the tree
13 -- starting from the root to leaves.
14
15 """
16
17 if not morph.getParentSMILES():
18 print("# Root #")
19 else:
20 print('# Morph #')
21 print('Parent:', morph.getParentSMILES())
22 print('SMILES: ', morph.getSMILES())
23 print('Descendents: ', morph.getDescendants())
24
25callback = MyCallback() # initialize a callback
26traverse = TraverseOper(callback=callback) # attach it to a tree traversal operation
27tree.runOperation(traverse) # run the operation
Output:
# Root #
SMILES: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
Descendents: ('COC(=O)C1C(COC(=O)C2=CC=CC=C2)C2CCC1N2C', 'COC(=O)C1C2CCC(CC1OC(=O)C1=CC=C(N)C=C1)N2C', 'COC(=O)CC1CCC(CCOC(=O)C2=CC=CC=C2)N1C')
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
SMILES: COC(=O)C1C(COC(=O)C2=CC=CC=C2)C2CCC1N2C
Descendents: ()
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
SMILES: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=C(N)C=C1)N2C
SMILES: COC(=O)CC1CCC(CCOC(=O)C2=CC=CC=C2)N1C
Descendents: ()
Descendents: ()
Note
The tree traversal algorithm uses multiple threads. Therefore, the output might appear a little messy.
In Listing 2.13 we derive from the TraverseCallback class, an abstract class with
an abstract method __call__(). This method takes one argument,
which is a MolpherMol instance
of a molecule in the tree. We need to override this method in our derived class in order to implement our own
behaviour.
The callback is then associated with a TraverseOper
instance, which can be run on a tree as any other
tree operation. When the operation is run it traverses the tree from the root to the leaves and injects
every molecule it encounters into our implementation of the
__call__() method.
Note
We can also pass a SMILES string to the TraverseOper
constructor. In that case, a subtree will be traversed
using the specified molecule as the root of the subtree.
There is also a much more convenient way to traverse the tree. Because, the ExplorationTree class implements
the molpher.core.ExplorationTree.ExplorationTree.traverse() method, we can simply take any python callable and use it instead of the
__call__() method.
However, under the hood it does the same thing as we did in Listing 2.13.
Therefore, the above code can be turned into:
1def process(morph):
2 """
3 Prints some information
4 about the molecules in the tree.
5
6 """
7
8 if not morph.getParentSMILES():
9 print("# Root #")
10 else:
11 print('# Morph #')
12 print('Parent:', morph.getParentSMILES())
13 print('SMILES: ', morph.getSMILES())
14 print('Descendents: ', morph.getDescendants())
15
16tree.traverse(process) # use the traverse method to run the callback function
Output:
# Root #
SMILES: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
Descendents: ('COC(=O)C1C(COC(=O)C2=CC=CC=C2)C2CCC1N2C', 'COC(=O)C1C2CCC(CC1OC(=O)C1=CC=C(N)C=C1)N2C', 'COC(=O)CC1CCC(CCOC(=O)C2=CC=CC=C2)N1C')
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
SMILES: COC(=O)CC1CCC(CCOC(=O)C2=CC=CC=C2)N1C
Descendents: ()
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
SMILES: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=C(N)C=C1)N2C
Descendents: ()
# Morph #
Parent: COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C
SMILES: COC(=O)C1C(COC(=O)C2=CC=CC=C2)C2CCC1N2C
Descendents: ()
2.4.3. Tree Templates and Snapshots¶
We don’t always have to initialize morphing parameters by hand. We can use an XML template instead.
Here is an example of a template file (you can download this one
from here):
1<!--
2 Template can be loaded instead of a snapsthot to initilize a tree.
3 It only contains information about the morphing parameters, however.
4
5 IMPORTANT: The name of a template file must end with '-template.xml'.
6 Otherwise it will be interpreted as a snapshot and the resulting tree
7 will be invalid.
8-->
9<iteration>
10 <source>
11 <smile>CN1[C@H]2CC[C@@H]1[C@@H](C(=O)OC)[C@@H](OC(=O)c1ccccc1)C2</smile>
12 </source>
13 <target>
14 <smile>O=C(OCCN(CC)CC)c1ccc(N)cc1</smile>
15 </target>
16 <fingerprint>FP_MORGAN</fingerprint>
17 <similarity>SC_TANIMOTO</similarity>
18 <param>
19 <nonProducingSurvive>2</nonProducingSurvive>
20 <acceptMin>50</acceptMin>
21 <acceptMax>100</acceptMax>
22 <farProduce>80</farProduce>
23 <closeProduce>150</closeProduce>
24 <farCloseThreashold>0.15</farCloseThreashold>
25 <maxMorhpsTotal>1500</maxMorhpsTotal>
26 <nonProducingSurvive>2</nonProducingSurvive>
27 <weightMin>0.0</weightMin>
28 <weightMax>500.0</weightMax>
29 </param>
30</iteration>
An XML template is similar to a configuration file and can be loaded just like a snapshot (see Listing 2.17), but the resulting tree will only contain the source molecule as its root.
1template_file = 'cocaine-procaine-template.xml'
2
3tree = ETree.create(template_file)
4print(tree.params)
5
6# apply the tree operations
7for oper in iteration:
8 tree.runOperation(oper)
9
10print(
11 sorted( # grab the new leaves as a list sorted according to their distance from target
12 [
13 (x.getSMILES(), x.getDistToTarget())
14 for x in tree.leaves
15 ], key=lambda x : x[1]
16 )
17)
18
19# save the tree in a snapshot file
20tree.save('snapshot.xml')
Output:
The new iteration has been created from template:
source: CN1[C@H]2CC[C@@H]1[C@@H](C(=O)OC)[C@@H](OC(=O)c1ccccc1)C2
target: O=C(OCCN(CC)CC)c1ccc(N)cc1
{
'max_morphs_total': 1500,
'far_close_threshold': 0.15,
'weight_max': 500.0,
'close_produce': 150,
'fingerprint': 'MORGAN',
'accept_min': 50,
'source': 'COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C',
'target': 'CCN(CC)CCOC(=O)C1=CC=C(N)C=C1',
'weight_min': 0.0,
'non_producing_survive': 2,
'accept_max': 100,
'operators': (
'ADD_ATOM',
'ADD_BOND',
'BOND_CONTRACTION',
'BOND_REROUTE',
'INTERLAY_ATOM',
'MUTATE_ATOM',
'REMOVE_ATOM',
'REMOVE_BOND'
),
'far_produce': 80,
'similarity': 'TANIMOTO'
}
Generated 66 morphs.
[('CN1C2CCC1C(C(=O)OCN)C(OC(=O)C1=CC=CC=C1)C2', 0.7777777777777778), ('CCN1C2CCC1C(C(=O)OC)C(OC(=O)C1=CC=CC=C1)C2', 0.7936507936507937), ('CN1C2CCC1C(C(=O)ON)C(OC(=O)C1=CC=CC=C1)C2', 0.8064516129032258)]
In the above example we loaded an XML template, created a tree from it, extended the tree and serialized it as a snapshot. We can see that all the parameters are the same as in the XML template and that the resulting tree can be built using the same list of operations as in Listing 2.12.
In Listing 2.16 we also serialized our tree instance to disk
with the save() method.
The saved tree can be later reconstructed with the
create() factory method:
1new_tree = ETree.create('snapshot.xml') # create a new tree from the saved snapshot
2print(new_tree.params)
3print(
4 sorted( # grab the leaves in the created tree (these should be the same as those in the original tree)
5 [
6 (x.getSMILES(), x.getDistToTarget())
7 for x in new_tree.leaves
8 ], key=lambda x : x[1]
9 )
10)
Output:
Snapshot successfully created from: snapshot.xml
{
'max_morphs_total': 1500,
'far_close_threshold': 0.15,
'weight_max': 500.0,
'close_produce': 150,
'fingerprint': 'MORGAN',
'accept_min': 50,
'source': 'COC(=O)C1C2CCC(CC1OC(=O)C1=CC=CC=C1)N2C',
'target': 'CCN(CC)CCOC(=O)C1=CC=C(N)C=C1',
'weight_min': 0.0,
'non_producing_survive': 2,
'accept_max': 100,
'operators': (
'ADD_ATOM',
'ADD_BOND',
'BOND_CONTRACTION',
'BOND_REROUTE',
'INTERLAY_ATOM',
'MUTATE_ATOM',
'REMOVE_ATOM',
'REMOVE_BOND'
),
'far_produce': 80,
'similarity': 'TANIMOTO'
}
[('CN1C2CCC1C(C(=O)OCN)C(OC(=O)C1=CC=CC=C1)C2', 0.7777777777777778), ('CCN1C2CCC1C(C(=O)OC)C(OC(=O)C1=CC=CC=C1)C2', 0.7936507936507937), ('CN1C2CCC1C(C(=O)ON)C(OC(=O)C1=CC=CC=C1)C2', 0.8064516129032258)]
2.4.4. Summary¶
Hopefully, you now have a very decent idea about what Molpher-lib can do and how to use it. If you have questions, bug reports or any suggestions on how to improve it, consider submitting them to the issue tracker. Any help on the project is much appreciated.